普通高中课程标准实验教科书 英语必修5 Unit 1 Great scientists
时间:2009-09-23 02:33:31
搜索关注在线英语听力室公众号:tingroom,领取免费英语资料大礼包。
(单词翻译)
Do you like puzzles? Euler did. Did you solve the one you heard for the listening task? No! Well, don't worry, Euler didn't either! As he loved mathematical1 puzzles, he wanted to know why this one wouldn't work. So he walked around the town and over the bridges of K6nigsberg several times. To his surprise, he found that he could cross six of the bridges without going over any of them twice or going back on himself (see Fig2 3), but he couldn't cross all seven. He just had to know why. So he decided3 to look at the problem another way. He drew himself a picture of the town and the seven bridges like the one above. He marked the land and the bridges. Then he put a dot or point into the centre of each of the areas of land. He joined these points together using curved4 lines to go over the bridges (see Fig 1). He noticed that some points had three lines going to them (A, B and C) and one had five (D). He wondered if this was important and why the puzzle would not work. As three and five are odd5 numbers he called them "odd" points. To make the puzzle clearer he took away the bridges to see the pattern more clearly (see Fig 2).
He wondered whether the puzzle would work if he took one bridge away (as in Fig 3). This time the diagram6 was simpler (as in Fig 4). He counted the lines going to points A, B, C and D. This time they were different. Two of them had even numbers of lines (B had two and D had four). Two and four are both even numbers so Euler called them "even" points. Two points in Fig 4 had an odd number of lines going to them (A and C both had three) and so he called them "odd" points.
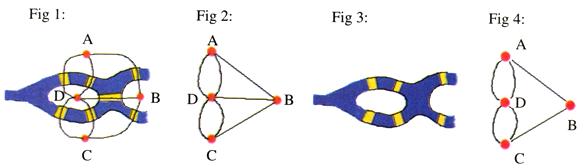
Using this new diagram Euler started at point A, went along the straight line to B and then to C. Then he followed the curved line through D and back to A. Finally he followed the other curved line from A back through D to C where he finished the pattern. This time it worked. He had been able to go over the figure visiting each point but not going over any line twice or lifting his pencil from the page. Euler became very excited. Now he knew that the number of odd points was the key to the puzzle. However, you still needed some even points in your figure if you wanted it to work. So Euler looked for a general rule:
If a figure has more than two odd points, you cannot go over it without lifting your pencil from the page or going over a line twice.
Quickly he went to his textbooks to find some more figures. He looked at the four diagrams7 shown below and found that when he used his rule, he could tell if he could go over the whole figure without taking his pencil from the paper. He was overjoyed. He did not know it but his little puzzle had started a whole new branch of mathematics8 called "topology". In his honour this puzzle is called "finding9 the Euler path".

 收听单词发音
收听单词发音 




